This article is published by China Science Software Network. If you have any questions, please contact us.
This case study is based on Valuing Employee Stock Options: Under 2004 FAS 123R (see Wiley Finance, 2004). Here we use the FASB software, which is used to create an example of the evaluation in the A87 part of the FAS 123R.
Administrative summary
In December 2004, the FASB published the final revised National Financial Accounting Standards 123 (FAS 123R, also referred to as FAS 123), which revised the FAS 123 and 95 issued in October 1995 for equity-based payments. This is considered by Wall Street to be the most far-reaching action of the Financial Accounting Board (FASB) in its 30-year history. The Act stipulates that from June 15, 2005, all new and partial existing employee stock options will be charged to the accounting books at cost. As expected by this standard, many companies (such as GE and Coca-Cola) have voluntarily included ESOs in their costs; hundreds of other companies still value their ESOs.
The purpose of this case study is to give the reader a better understanding of the valuation of the method chosen by FAS 123 (binary tree model). We will systematically and purposefully evaluate the method and compare it to the results of the Black-Scholes Model (BSM). This case study shows that FAS 123 can make accurate estimates. The analysis here uses a traditional binary tree model and considers what might happen under realistic conditions (eg, the right to retain a pension, the behavior of an employee choosing a suboptimal plan, the rate of void, the ESO fluctuations throughout the statement process) Sex). This case introduces the concept of FAS 123 and gives different ESO valuation methods (closed form of BSM, binary tree, Monte Carlo simulation) and their effects. We have found that by using the right approach to meeting FAS 123 requirements, companies can reduce the cost of millions of dollars per year. This avoids unnecessary valuation of naive BSM and uses a modified custom binary tree model (which takes into account accounting sub-optimal behavior, void rates, retention of pension rights, date of interruption) The input value that changes with time).
Introduction
Under the conditions that meet the requirements of FAS 123, the method chosen to calculate the fair market ESO valuation is a binary tree model, but critics believe that companies do not have internal resources and data to run complex valuations (this valuation is Comply with the new requirements and be able to pass the review). Based on the author's research report submitted to the FASB Board of Directors in 2003, we can conclude that BSM is theoretically correct and beautiful, but when it is applied to the quantitative analysis of ESOs valuations in fair markets, it It neither applies nor is correct. This is because BSM only applies if there is no bonus for European options (the holder of European options will only execute the option when the option expires and the potential stock will not be able to pay any dividends). However, in reality most ESOs are American options with dividends (the option holder can execute the option at any point in time including the expiration date and the potential stock pays the dividend). In addition, under realistic conditions, ESOs allow employees to have the right to wait for options before they execute an option, which can happen at any time in the company. This is because employees may leave the company early or end before the scheduled period. In addition, some options have a tranching or graduated scale so that a certain percentage of stock options will be executed each year. Similarly, some employees will exhibit irrational behavior, they only execute the option when the option value exceeds the contract price several times, that is, they choose the sub-optimal behavior. On the other hand, the value of the option may be sensitive to the desired economic environment. Since the interest rate has a term structure, the risk-free rate may change during the life of the option. Finally, some companies may undergo restructuring (asset divestiture, mergers, acquisitions will affect the volatility of the underlying stock). With these factors in mind, when BSM is applied to the fair market, it does not seem appropriate or appropriate. In general, companies can implement a range of actions that affect the value of options. A closed form model (such as BSM) or a general Black-Scholes model (GBM) (the latter requires bonus benefits) is unstable and cannot be modified to fit the real environment. Therefore, we choose the binary tree model.
Under certain conditions (European options without dividends), the results obtained using the binary tree model and Monte Carlo simulation are the same as those obtained with BSM, indicating that the first two methods are excellent and the limits are accurate. However, when specific conditions change (probability of voiding, probability of employee turnover or suspension of working time, selection of suboptimal behavior), only the binary tree model is highly stable and can give a fair market value for ESO. BSM only considers the following input information: stock price, contract price, maturity date, risk-free interest rate, and volatility. GBM considers all of the above input values ​​and the distribution rate of dividends. Therefore, according to the requirements of FAS 123, BSM and GBM are not suitable for real life. In contrast, the binary tree model can be modified to include stock prices, contract prices, maturities, single risk-free rates (or multiple risk-free rates that change over time), single volatility (or multiple changes over time) Volatility), single dividend distribution rate (or multiple dividend distribution rate that changes over time), all real-world factors (mainly: conversion cycle, sub-optimal behavior of early execution of options, interruption cycle, scrap rate, stock price, and performance) Obstacles, other possibilities for abnormalities). We note that if we ignore these real-world conditions, the results obtained using the binary tree model are the same as those obtained using GBM.
The most important and convincing argument for the binary tree model is as follows: 1FASB needs it and considers the binary tree model to be a good way to evaluate ESO. 2 The binary tree model can greatly reduce the cost of ESO by appropriately reflecting the actual conditions. The following is an example of FAS 123, which is intended to explore the use of a binary tree model.
B64. As discussed in A10-A17, a closed-form model is a method that can be used to predict the fair market value of employee stock options. However, the binary (multi) fork tree model can be adapted to the term structure of the risk-free rate, the expected volatility, and the expected dividend change before the option expires. The two (multiple) cross-tree model can also be adapted to estimate the employee's model of executing options, options within the expiration date, etc., and thus better reflect these factors.
A15. The Black-Scholes-Merton formula assumes that options can only be executed on the expiration date of the option, and the expected volatility, expected dividends, and risk-free interest rates remain constant throughout the life of the option. If it is used to estimate fair value, then the Black-Scholes-Merton formula needs to be modified to take into account the contradiction between the actual employee stock options and the model's assumptions (eg, the option is executed before the maturity date). ability). Due to the nature of this formula, those adjustments take the form of a weighted average of the different hypotheses. In contrast, the two (multiple) fork tree model can dynamically adjust the dividends during the option's validity period, the prediction of the option execution mode, and the impact of the outage period. Therefore, the two (multi) fork tree model can effectively simulate the different characteristics of various employee stock options. However, the two (multiple) fork tree model, the Black-Scholes-Merton formula, and other valuation techniques that satisfy the A8 segment can give an estimate of fair value. However, if an entity uses a calibrated model (taking into account the following factors: the contractual duration of the option, the way the employee expects to perform, and the hiring abort after the wait), the estimate of the expected duration is based on two (multiple) The output of the fork tree model. For example, an entity's experience may indicate that the holder of the option tends to execute the option after the stock price has doubled. If so, the entity may use a two (multi) fork tree model that assumes that when the expected condition for executing the option is met, the option is executed at each node of the stock price path (if the option can wait at that node and can be carried out). In addition, when the expected condition for executing an option is not met and the option is still in a real-value state after the contract expires, the model also assumes that the option is executed after the expiration. This approach suggests that employee performance is related to potential prices. This model also considers the employment suspension behavior after the option is awaited. Based on the resulting two (multiple) cross-tree model (see paragraph A240), we can estimate the expected duration.
In fact, some parts of FAS 123 cannot be considered in the traditional Black-Scholes model. The two (multi) fork tree model needs to model the following factors: suboptimal execution behavior, invalidation rate, option wait, interrupt period, and so on. The results of this case study and software calculations used a two (three) cross-tree model, a closed-form Black-Scholes model to compare the results. The FAS 123 paragraph describing the use of the two (multi) fork tree model includes the following entries:
A27. However, if an entity uses a calibrated model (taking into account the following factors: the contractual duration of the option, the manner in which the employee expects to perform, and the hiring abort after the waiting), the estimate of the expected duration is based on two ( Multi) The output of the fork tree model. For example, an entity's experience may indicate that the holder of the option tends to execute the option after the stock price has doubled. If so, the entity may use a two (multi) fork tree model that assumes that when the expected condition for executing the option is met, the option is executed at each node of the stock price path (if the option can wait at that node and can be carried out).
A28. Other factors that affect the employee's performance of the option and the hiring of the suspension after waiting include:
Reward for the waiting period. The expected duration of the option should include at least the waiting period.
The historical execution of the employee and the suspension of employment after waiting.
Expected volatility of the underlying stock price.
Interruption period and other arrangements (for example, when certain conditions are met, the option is automatically executed).
The age of the employee, the length of the term of employment, and the domestic judicial situation.
Therefore, based on the aforementioned judicial system and the requirements and recommended conditions for the revised FAS 123 (which chooses the binary tree model), we can think that the binary tree model is the best and most recommended method for calculating the fair value of ESOs.
Use of preferred methods
When using the modified binary tree model, you need to judge the following input values:
The stock price on the approval date.
The contract price of the approved option.
The expiration time of the option.
Risk-free interest rates for the option life cycle.
Dividend income of the stocks in the option life cycle.
Volatility in the life cycle of an option.
The waiting period for the option.
Sub-optimal execution behavior in the option life cycle.
Obsolete rate and employee mobility in the option life cycle.
The date of the interruption after waiting for the option to be executed.
This analysis assumes that an employee cannot execute an option while the option is waiting. Further, if the employee's working life is terminated and the decision to wait for the period to voluntarily leave, the approval of the option will be invalidated and considered to be worthless. In contrast, after the option waiting period, employees tend to behave irrationally in the execution of options, a sub-optimal behavior. However, if an employee voluntarily leaves or suspends employment, the waiting option must be executed within a short period of time (regardless of suboptimal behavior, ie, option failure occurs, which is caused by the failure rate of the option and the employee's migration. Rate to measure). Finally, when the option expires, if the option is in real value, it will be executed; if it is in a virtual or two-flat state, the option will expire. The next section will detail the results of this case study.
ESO valuation package
In theory, we can also estimate the large-scale binary tree model ESO without software. The software used in this analysis is the employee stock option valuation toolkit 1.1 (see Figure 1.1) written by the author of this book. The FASB also uses this software to prove that the ESO valuation is effective and operational. In fact, FASB used this software to calculate and evaluate the final example of the A87-A88 segment of FAS 123. Figure 1.2 An example module of a custom American option that uses a binary tree model with waits, failure rate, sub-optimal execution behavior, risk-free interest rates and volatility over time. Real Options Super Lattice software can also be used to create any custom ESO model using the binary tree model and FASB preference.

Figure 1.1 ESO Valuation Toolkit 1.1 Software
This software shows how to use closed-form models (such as BSM/GBM) and binary tree models. With the binary tree model, we can solve more complex ESO problems. For example, a custom advanced option (see Figure 1.2) shows multiple variables (risk-free interest rates, dividends, volatility, failure rates, sub-optimal execution behavior, etc.) over time. In addition, for increased instability, the Super Lattice Solver module allows us to solve custom ESO problems. This feature allows management to experiment with different styles of ESO to find the ones they need to minimize the cost of equity holders.
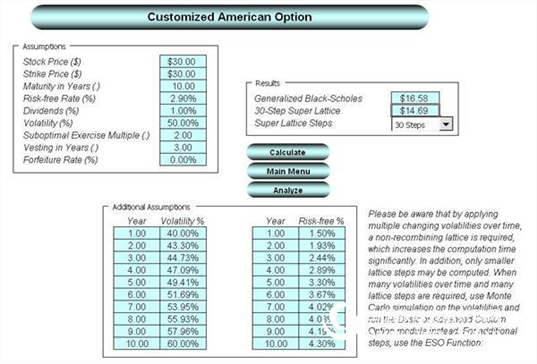
Figure 1.2 Customized Advanced Option Model
Figure 1.2 shows an example solution for the A87 paragraph of the final FAS 123 guideline of 2004. Specifically, A87-A88 is as follows:
A87. The table below shows some assumptions and related information about stock options approved on January 1, 2005.
Stock options totaled 900,000.
The employee's options total 3000.
The stock price on the approval date is $30.
The execution price is $30.
The contract period (CT) is 10 years.
The risk-free rate during the contract period is 1.5% to 4.3%.
The expected volatility during the contract period is 40% to 60%.
The expected dividend income during the contract period is 1.0%.
The suboptimal execution multiplier is 2.
A88. This example assumes that each employee is approved to have 300 options. By selecting 7 items from the above list as output values, we can conclude that the fair value of each option is $14.69. This model uses a suboptimal execution multiplier to calculate the desired item (ie, the desired item as the output value) instead of using the desired item as an isolated input value. If the Black-Scholes-Merton option pricing formula is used, the desired item should be used as an input value rather than a sub-optimal execution multiplier.
Figure 1.2 shows the result of $14.69, which FASB used in its example. In the FASB example, a 3% failure rate is applied outside the model to discount the amount that is reduced over time. This software allows us to enter the failure rate inside or outside the model (before or after waiting). In this example, we set the failure rate to 0 (Figure 1.2) and exclude the quantity, as the FASB did in A91: the number of stocks expected to be awaited is estimated to be 821406 (900000× on the approval date). 0.973).
In fact, using ESO's valuation package and Excel's target exploration function, we can see that the expected life cycle of this option is 6.99 years. If you enter 6.99 into the corrected GBM, then we can get the same result of $14.69 (this is not possible without the binary tree model).
Technical proof of the method used
This section describes the technical proof of the price difference between GBM and a custom binary tree model. Figure 1.3 shows how each input variable is derived in a custom binary tree model. Based on this graph, it is clear that volatility is not a key variable in the value of an option. In fact, when the elements such as wait, failure, and suboptimal behavior are considered into the model, their effects control the volatility. This figure shows a typical case and cannot be used as a generalized case.
In contrast, in a simple BSM, volatility is a significant variable (as shown in Figure 1.4). This is because the input variables have less interaction due to fewer variables being input. For many ESOs in a two-flat state, volatility plays a very important role when there are no other dominant input variables.
In addition, the interaction of these new input variables is non-linear. As can be seen from Figure 1.5, waiting, failure rate, and suboptimal behavior are nonlinear in the option value. That is, the lines in the figure are not straight but appear curved in some parts, which indicates that there is a nonlinear influence in the model. This suggests that in the value of the option, we cannot generalize the three variables (for example, we can not sum up as follows: for every 1% increase in failure rate, the value of the option will be reduced by 2.35%; this means that each failure rate increases 2%, the value of the option will drop by 4.7%). This is because at different levels, the interaction of variables is different. We can sum up as follows: It is not possible to draw general conclusions about the effects of changes in a variable. For each case, more details are analyzed.
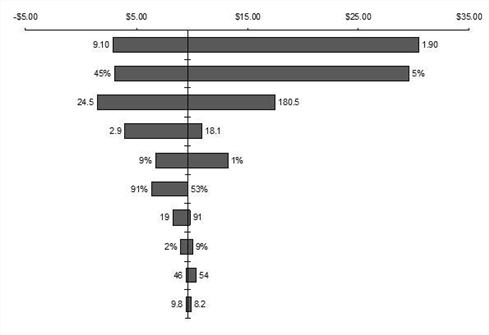
Figure 1.3 The hurricane chart shows the key input factors in the custom binary tree model.
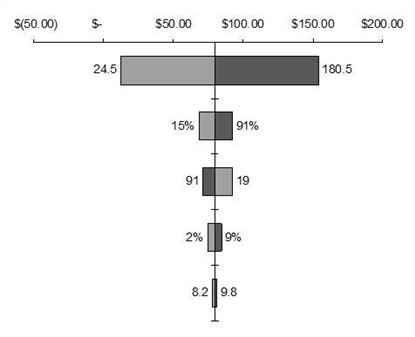
Figure 1.4 The hurricane chart shows the key input factors in the BSM model,
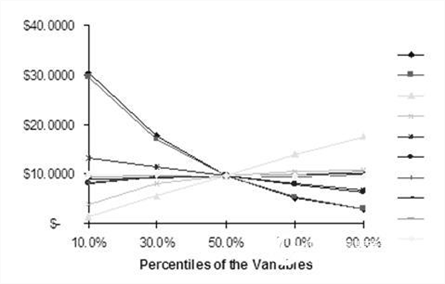
Figure 1.5 The spider graph shows the nonlinear effects of the input variables in the binary tree model.
Although each graph shows the effect of changes in the input value of the variable on the value of the option, that is, the effects are static. However, as shown in Figure 1.5, these effects are often non-linear, which means that we need to change the values ​​of the variables at the same time to find out their interaction. Figure 1.6 shows the dynamic sensitivity of Monte Carlo simulations, where failure rate, waiting, and suboptimal behavior are considered important variables, and volatility is once again considered a secondary variable. The graph of dynamic sensitivity is obtained after thousands of changes to the value of the input variable, which captures the effect of the change in the value of the option. This approach is very valuable in capturing the net interaction of the input values ​​of different variables.
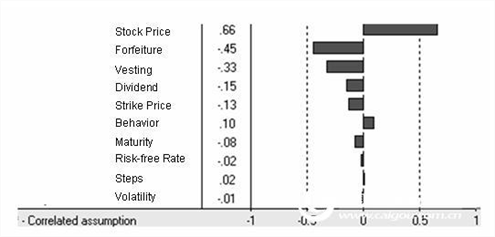
Figure 1.6 Dynamic sensitivity analysis of simultaneous changes in input variables
From these sensitivities analysis, we can conclude that combining the failure rate, waiting, and suboptimal behaviors is very important for obtaining the fair value of ESOs because they have a significant impact on the value of the options. In addition, we cannot generalize the input variables that have an impact on the value of the option. In order to get the value of the option, we have to do a specific analysis every time.
Option with pending and sub-optimal execution
By further studying suboptimal behavior and waiting, we obtained the results shown in Figure 1.7. Here we find that under the lower incidence of suboptimal behavior, the stock option value is significantly lower than the value predicted by BSM. For a 10-year waiting stock option, the two results are the same. This is because for an option that waits for 10 years and expires in 10 years, it will be converted to a European option and can only be executed on the expiration date. In this case, BSM gives the correct result.
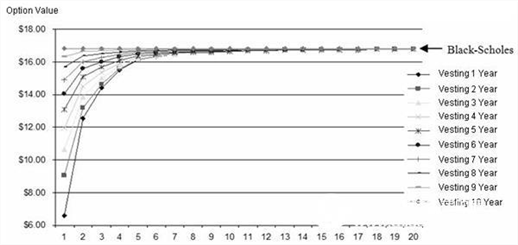
Figure 1.7 Effect of sub-optimal execution behavior and waiting period on option value
(Usage hypothesis: stock price and execution price are 25 US dollars, maturity is 10 years, risk-free rate is 5%, volatility is 50%, bonus rate is 0%, sub-optimal performance multiplier is 1~20, wait The right period is 1~10 years, and the binary grid attempt of 100~5000 steps is performed)
However, when the incidence of suboptimal behavior decreases, the value of the option will decrease. This is because employees holding options tend to execute options in a sub-optimal way, ie they execute the option before the stock price reaches its optimal value. Therefore, the value of the option is not maximized. For example, if the contract price of an option is $10, the underlying stock has high volatility. If an employee executes an option with $11 (the sub-optimal execution multiplier is 1.1), he is not able to effectively grasp the price increase space brought by the high volatility of the underlying stock. Suppose another employee executed an option at a stock price of $20 (the sub-optimal execution multiplier is 2.0). Therefore, lower sub-optimal execution behavior means lower fair value of stock options. When the stock price of the forecasted approval date is higher, the sub-optimal execution behavior has a higher impact on the stock. Figure 1.8 shows that the closer to the approval date, the higher the slope of the curve.
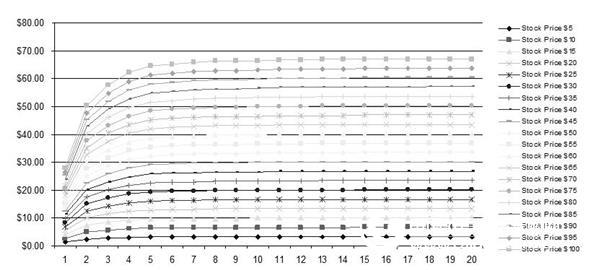
Figure 1.8 The effect of sub-optimal execution behavior and stock price on the value of options
(Usage hypothesis: stock price and execution price range is 5~100 USD, maturity period is 10 years, risk-free rate is 5%, bonus rate is 0%, sub-optimal performance multiplier is 1~20, waiting period is 4 years, carry out a binary grid test of 100~5000 steps)
Figure 1.9 shows that the higher the stock volatility, the larger the suboptimal area and the greater the impact on the value of the option, but the effect is asymptotic. For example, for stocks with 100% volatility, the suboptimal region extends from the suboptimal execution multiplier of 1.0 to the suboptimal execution multiplier of 9.0 (for stocks with a volatility of 10%, suboptimal regions). The extension from the suboptimal execution multiplier to 1.0 is extended to the suboptimal execution multiplier of 2.0. In addition, 100% volatility stocks fluctuate from $12 to $22 with a volatility of $10 (and 8% volatility stocks fluctuate from $2 to $10 with a volatility of $8). Therefore, the higher the stock price on the approval date, the higher the volatility, and thus the sub-optimal behavior has a higher impact on the option value. In each case, the results of the BSM appear as horizontal lines in the figure (Figure 1.8, Figure 1.9). That is, BSM assumes that all behaviors are optimal, so it always maximizes the value of the option, which significantly overestimates the value of the option. Both GBM and BSM cannot take into account sub-optimal execution behavior, and only the binary tree model can do this.
Option with failure rate
Figure 1.10 shows that as the failure rate increases, the option value decreases. The reduced ratio depends on the waiting period. The longer the waiting period, the greater the effect of failure rate on the value of the option, which indicates a nonlinear interaction relationship between waiting and failure (the lines in Figure 1.10 are curved and non-linear). Intuitively we can perceive this, and the longer the waiting period, the higher the likelihood that an employee will continue to accept employment and the higher the likelihood of failure. This will reduce the expected value of the option.
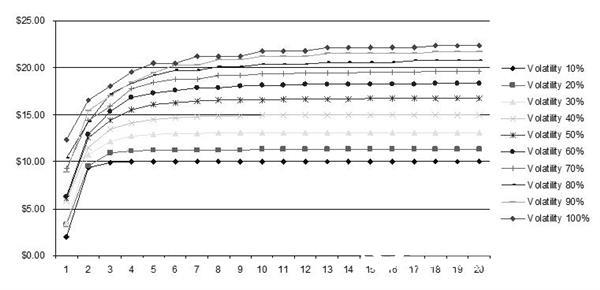
Figure 1.9 Effect of sub-optimal execution behavior and volatility on option value
(Usage hypothesis: stock price and strike price are $25, maturity is 10 years, risk-free rate is 5%, volatility is 10%-100%, bonus rate is 0%, sub-optimal performance multiplier is 1~ 20, the waiting period is 1~10 years, and the binary grid test of 100~5000 steps is performed)
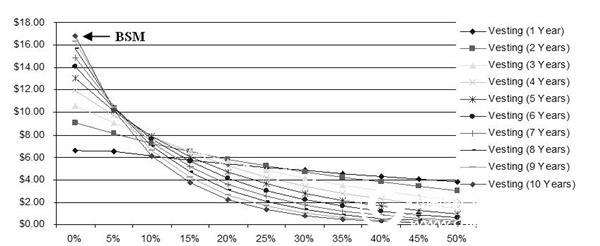
Figure 1.10 Effect of penalty rate and waiting period on option value
(Usage hypothesis: stock price and execution price are 25 US dollars, maturity period is 10 years, risk-free rate is 5%, volatility is 50%, bonus rate is 0%, sub-optimal performance is 1.01, waiting period is 1 ~10 years, the penalty rate is 0~50%, and the binary grid test of 100~5000 steps is performed)
Once again, we can note that for an option with a 10-year waiting period, a 10-year validity period, and a 0 failure rate, BSM will always have a high valuation (Figure 1.10). In addition, if the company is functioning properly and the stock price tends to rise, which makes the option more valuable and makes it less likely that the employee will leave the company and the company is less likely to dismiss the employee – the stock price and failure rate will have Negatively related features. Because of the uncertainty of failure rate (in the past, failure rate usually fluctuated with changes in the economic environment, and it will fluctuate in the future) and has a negative correlation with stock prices, we can have a correlation with Monte. Carlo simulations are used for failure rates and can be used in conjunction with a binary tree model (explained later in this case study). BSM always maximizes the value of the option. The ESO estimation software can take into account the failure rate. The Super Lattice Solver can take into account the different pre- and post-failure failure rates in the two (multi) fork tree model.
Options for risk-free interest rates that change over time
Another assumption of the input value is the risk-free rate. Figure 1.11 shows the effect of risk-free interest rates over time on the value of options. When other input values ​​are added, the two (multiple) fork tree model with no risk-free interest rate will underestimate the option value as a whole. In addition, given the time value of money, a higher discount on future cash flows will reduce the value of the option. Figure 1.11 compares the slope-increased yield curve and the slope-reduced yield curve, which appear on the image as the crescent with the opening up and the crescent with the opening facing down. When the term structure of the interest rate increases over time, the option value calculated using the non-constant risk-free rate binary tree model ($24.31) is lower than the average value calculated using the risk-free rate ($25.92). For the reduced term structure, the opposite is true. In addition, Figure 1.11 shows the risk-free interest rate curve with the opening down (the interest rate is low first, then the high then the low) and the risk-free interest rate curve with the opening up (the interest rate is high first, then low and then high). This result suggests that using a simple averaging approach would overestimate the yield curve for slope increases and underestimate the yield curve for slope reduction. Therefore, we should make changes to the risk-free rate over time.
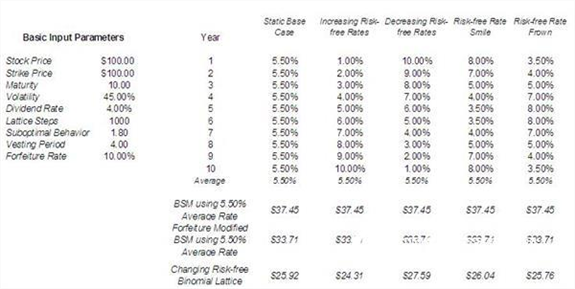
Figure 1.11 Effect of changing risk-free interest rates on option value
These results can only be used to illustrate a typical situation and cannot be used in all cases as a generalized example.
Volatility options over time
Figure 1.12 shows the effect of fluctuations in ESO over time. If volatility changes over time, BSM ($71.48) with average volatility will always overestimate the value of the option when there are other input variables. In addition, comparing it to $38.39 in the underlying condition, volatility that slowly increases from a lower level over time will result in lower option value, while volatility decreases from a higher level (and when volatility The performance is expressed as a crescent with the opening up or down), and the calculated result is higher than the result calculated by the average volatility.
Options for dividends that change over time
Dividend income is a relatively simple input data that we can obtain from a company's dividend distribution policy or historical data. When we calculate the bonus income, we add up the bonuses in the year to calculate the ratio of the total dividend to the stock price. Usually dividend income is between 0% and 7%. In fact, about 45% of listed companies in the United States pay dividends. Among the companies that pay dividends, 85% of the dividends are less than 7%, and 95% of the dividends are less than 10%. Bonus yield is a very interesting variable that has a small correlation with other input variables. It has a nearly linear effect on the value of the option, while other input variables do not. For example: Figure 1.13 shows the effect of different expiration dates for the same option. The longer the maturity period, the higher the option value, but the option value growth rate is decreasing.
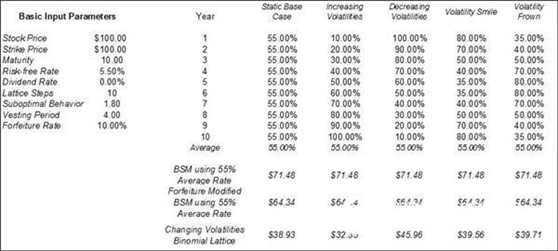
Figure 1.12 The effect of varying volatility on option value
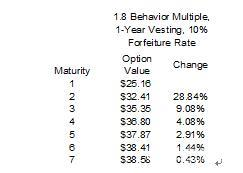
Figure 1.13 Non-linear effects of maturity
(Usage hypothesis: stock price and execution price are $100, maturity is 10 years, risk-free rate is 5%, volatility is 75%, custom grid steps are 1000 steps, sub-optimal execution behavior multiplier is 1.8, The waiting period is 1 year and the penalty rate is 10%.
In contrast, Figure 1.14 shows that even when other input variables change, the effect of the bonus is still nearly linear. Regardless of the change in the variables, the impact of the dividend on the option is nearly linear. Figure 1.14 shows a number of options with special bonus rates. Figure 1.15 shows the effect of a single option's dividend over time. The results in Figure 1.14 are derived by comparing different options with different red interest rates. The results in Figure 1.15 are derived by comparing the effects of a single option with a red interest rate change over time.
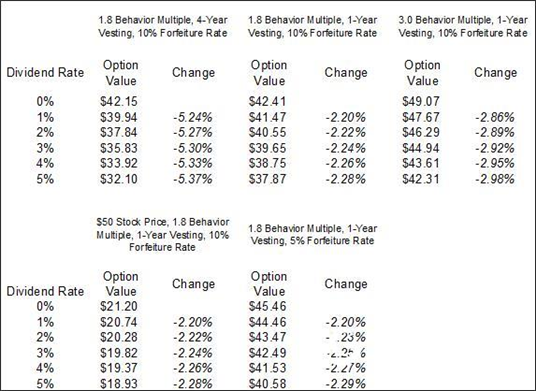
Figure 1.14 The near linear effect of the red interest rate

Figure 1.15 The impact of changing red interest rates
(Usage hypothesis: stock price and strike price are $100, maturity is 5 years, risk-free rate is 5%, volatility is 75%, custom grid steps are 1000 steps, sub-optimal execution behavior multiplier is 1.8, The waiting period is 1 year)
Obviously, if the dividend of an option changes constantly, it is valuable to the option. Therefore, if the company's stock pays dividends, then our analysis should consider the possibility of a change in the red interest rate.
Option with interruption period
Another interesting one is the interruption period, in which ESOs cannot be executed. This period is usually a few weeks before the announcement of revenue (usually a quarterly financial report), or it may be a few weeks later. In addition, only senior managers with the responsibility of the trustee have such an interruption option, so this part of the option is only a small part of the entire company. Figure 1.16 shows the results of a typical ESO with different outage periods. Some options have only a few days of interruption in a month, which is different from the normal option with a blackout period, and also different from those without an interruption period. In fact, if the suboptimal execution multiplier is small (assuming this value is 1.8 in this example), the policy's outage period will prevent the option holder from executing the option with suboptimal behavior and the value of the option will increase slightly.

Figure 1.16 Effect of the prohibition period on the value of options
(Usage hypothesis: stock price and execution price are $100, maturity is 10 years, risk-free rate is 5%, volatility is 75%, custom grid steps are 1000 steps, sub-optimal execution behavior multiplier is 1.8, No red interest rate, the waiting period is 1 year, the penalty rate is 10%)
The analysis shown in Figure 1.16 assumes that the interruption period in a year is only a small percentage (that is, only a few days in a year cannot perform ESO). For stock options of these companies, the break period can be ignored. However, for biotech companies, high-tech companies, etc., the deadline for interruption plays a very important role. For example, in a biotech company, the quarterly outage may be 4-6 weeks, which will span the time of the quarterly bulletin. In addition, an outage period may be set before new products are put into production. Therefore, the annual interruption period may account for 35% to 36% of the option life cycle. In this case, the interruption period will significantly affect the value of the option. For example, Figure 1.17 shows the difference between a custom binary tree model with an outage period and no interruption period. After the introduction of the interruption period, the value of ESO is reduced by 10% to 35% (the specific value depends on the volatility of the failure rate). As expected, the reduced value is non-linear because the effect of the interruption period varies with other different input variables in the analysis.
Figure 1.18 shows the effect of different waiting periods and different breakout periods for dividends, while Figure 1.19 shows the results for different dividend yields and sub-optimal execution multipliers. Obviously, we can only accurately predict the impact after specific analysis, which is generally 10% to 20%. Interruption periods can only be modeled using a binary tree model and cannot be used with BSM/GBM.
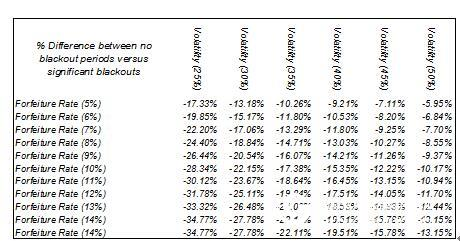
Figure 1.17 Effect of the prohibition period on the value of options (different penalty rates and volatility)
(Usage hypothesis: stock price and execution price are 30~100 USD, the volatility is 45%, the risk-free rate is 5%, the maturity period is 10 years, the red interest rate is 0%~10%, and the waiting period is 1~4 In the year, the penalty rate is 5% to 14%, the sub-optimal performance parameter is 1.8 to 3.0, and the number of grid steps is 1000.
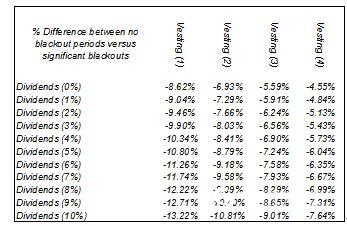
Figure 1.18 Impact of the key prohibition period on the value of options (different red interest rates and lockout periods)
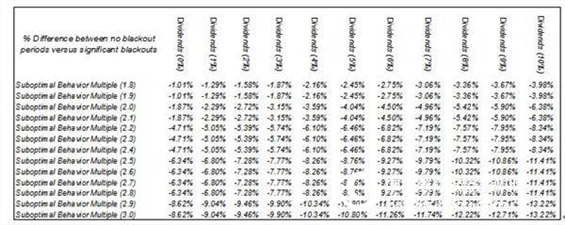
Figure 1.19 Impact of the Critical Prohibition Period on Option Value (Different Red Interest Rates and Execution Behavior)
Non-circulation problem
FAS 123 in 2004 did not explicitly discuss non-liquidity, that is, ESO can neither be directly transferred to other people nor freely traded in the market. In this case, based on reliable financial and economic theory, we can approximate the discount under non-circulating conditions to ESO. However, this is not an easy task.
A simple and straightforward application of discounting should not be the result of multiplying the arbitrarily chosen percentage by the binary tree model. We can use put options for more rigorous analysis. A call option is a contractual right, not an obligation, which allows the option holder to purchase the underlying stock at the contract price within a specified time; the put option is also a contractual right, not an obligation. It allows the holder of the option to sell the stock at the contract price within the specified time. Therefore, if an ESO holder cannot sell or wait for an option, holding it is equivalent to giving up the option to sell the option (ie, the employee has endorsed or sold the put option to the company).
However, we must be extra careful when encountering such discount features in our analysis.在计算看涨期æƒæ—¶è¾“入自定义二å‰æ ‘模型的输入值也åŒæ ·åº”该输入看跌期æƒã€‚å³çœ‹è·ŒæœŸæƒä¹Ÿå¿…须具有相åŒçš„风险(波动性会éšç€æ—¶é—´è€Œæ”¹å˜)ã€ç»æµŽçŽ¯å¢ƒ(æ— é£Žé™©åˆ©çŽ‡çš„æœŸé™ç»“构会éšç€æ—¶é—´è€Œæ”¹å˜)ã€åˆçº¦çš„义务(ç‰å¾…ã€åˆ°æœŸæ—¥ã€åˆçº¦ä»·æ ¼ã€ä¸æ–期é™)ã€æŠ•èµ„者的ä¸ç†æ™º(次优执行行为)ã€å…¬å¸çš„业绩(æ‰¹å‡†æ—¥çš„è‚¡ç¥¨ä»·æ ¼)ç‰ã€‚
尽管FAS 123没有明确地讨论ä¸å¯æµé€šæ€§ï¼Œå‡ºäºŽå®Œæ•´æ€§çš„考虑,我们在æ¤å¯¹ä»·å€¼è¿›è¡Œåˆ†æžã€‚åªæœ‰æ¯ä¸ªå…¬å¸çš„管ç†å±‚æ‰èƒ½å†³å®šæ˜¯å¦åº”该è¿ç”¨è´´çŽ°ã€‚图1.20显示的是è¿ç”¨è‡ªå®šä¹‰äºŒå‰æ ‘模型对ESO进行计算的结果。图1.21显示的是éžæµé€šæ€§çš„分æžç»“果,这是将相åŒçš„输入值(ç‰å¾…ã€ä¸æ–ã€å¤±æ•ˆã€æ¬¡ä¼˜è¡Œä¸ºç‰)输入自定义二å‰æ ‘模型而计算出的结果。贴现率的范围是22%~53%。这些贴现率看上去有些大,但它们其实是符åˆå¸‚场预期的。由于FASB没有明确地批准这些贴现率,所以作者建议在决定ESOçš„å…¬å…市场价值时è¦è°¨æ…Žã€‚
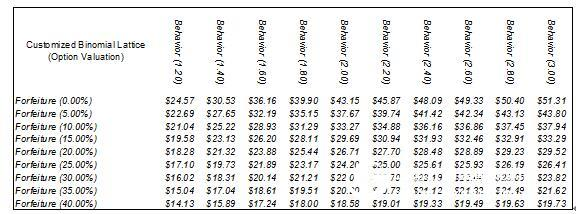
图1.20 定制二å‰ç½‘æ ¼æ¨¡åž‹ä¼°å€¼ç»“æžœ
(使用å‡è®¾ï¼šè‚¡ç¥¨ä»·æ ¼å’Œæ‰§è¡Œä»·æ ¼ä¸º100美元,æˆç†ŸæœŸä¸º10年,待æƒæœŸä¸º1年,波动率为35%,红利率为0%ï¼Œæ— é£Žé™©åˆ©çŽ‡ä¸º5%,次优执行行为å‚数为1.2~3.0,罚没率为0%~40%ï¼Œå®šåˆ¶ç½‘æ ¼æ¥æ•°ä¸º1000æ¥)
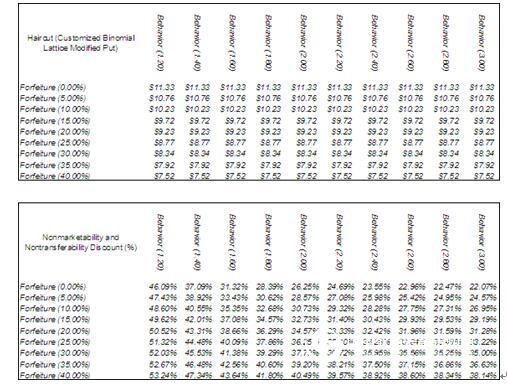
图1.21 ä¸å¯é”€å”®å’Œä¸å¯è½¬æ¢è´´çŽ°çŽ‡
寿命分æž(生å˜åˆ†æž)
æ£å¦‚å‰é¢æ‰€è®²åˆ°çš„é‚£æ ·ï¼Œ2004年最终的FAS 123çš„A15å’ŒB64ä¸å…许使用带有å•ä¸€æœŸæœ›ç”Ÿå‘½å‘¨æœŸçš„BSM。这æ„味ç€æˆ‘们ä¸èƒ½æŠŠæœŸæœ›çš„生命周期输入到BSMä¸ï¼Œä»Žè€ŒèŽ·å¾—类似自定义的二å‰æ ‘模型计算的结果。我们åªèƒ½å¦å¯»å®ƒæ³•ã€‚å³è¿ç”¨ç‰å¾…è¦æ±‚ã€æ¬¡ä¼˜æ‰§è¡Œä¹˜æ•°ã€å¤±æ•ˆçŽ‡ã€å‘˜å·¥æ›´æ›¿çŽ‡ä»¥åŠå…¶ä»–æ ‡å‡†æœŸæƒçš„输入值,通过自定义二å‰æ ‘模型计算出估值结果。这ç§ç»“æžœä¸Žæ ¡æ£åŽçš„BSM具有å¯æ¯”性,并且期望的生命周期å¯ä»¥ä½œä¸ºè¾“入值。通过将BSM的结果设置为与自定义的二å‰æ ‘模型相ç‰ï¼ŒExcelçš„ç›®æ ‡æœç´¢å‡½æ•°å¯ä»¥è¢«ç”¨æ¥èŽ·å–期æƒçš„期望的生命周期的输入值。期望的生命周期的输出结果å¯ä»¥ä¸ŽåŽ†å²æ•°æ®ç›¸æ¯”较,从而作为å¦ä¸€ç±»è¾“出结果,å³æœŸæœ›çš„生命周期是å¦åœ¨åŽ†å²æ•°æ®çš„范围之内。由于测度期æƒçš„期望的生命周期是éžå¸¸å›°éš¾çš„也是ä¸å‡†ç¡®çš„,故而这ç§æ–¹æ³•æ˜¯æ£ç¡®çš„。
如图1.22所示,通过将BSM的结果与自定义二å‰æ ‘模型的结果设置为相ç‰ï¼Œæˆ‘们å¯ä»¥å¯¹ESO Valuation Toolkit软件è¿è¡ŒExcelçš„ç›®æ ‡æœç´¢å‡½æ•°ï¼Œä»Žè€ŒBSM模型输入期望的生命周期。
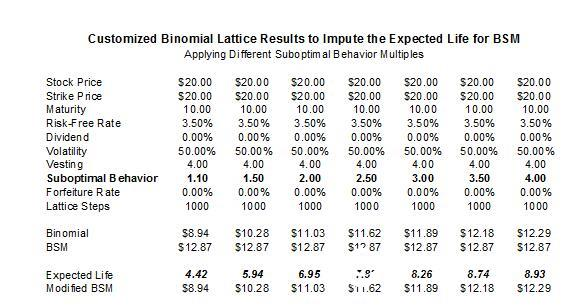
图1.22 使用二å‰æ ‘结果æ¥ç¡®å®šæœŸæƒé¢„期生命周期
图1.23显示的是å¦ä¸€ä¸ªä¾‹å,在æ¤å¤„期望的生命周期å¯ä»¥è¢«è¾“入,但失效率并ä¸ä¸º0。在这ç§æƒ…况下,需è¦å¯¹BSM的结果进行修æ£ã€‚例如:自定义二å‰æ ‘模型的结果为$5.41(失效率为15%)。这æ„味ç€ï¼Œå¦‚æžœè¿ç”¨ä¿®æ£çš„期望生命周期的方法,结果应该为BSM×(1-15%)=$5.41。期望的生命周期是2.22年,产生的BSM值是$6.36($5.41/85%=$6.36,$6.36×(1-15%)=$5.4)。
稀释
在大多数情况下,稀释的影å“å¯ä»¥å¿½ç•¥ä¸è®¡ï¼Œå› 为批准的ESOåªå å…¬å¸çš„期æƒæ€»é‡çš„很å°ä¸€éƒ¨åˆ†ã€‚在财务投资ç†è®ºä¸ï¼Œå¸‚场早已预期到了ESOsçš„æ‰§è¡Œï¼Œå¹¶ä¸”è‚¡ç¥¨ä»·æ ¼ä¹Ÿå·²ç»åæ˜ äº†å®ƒçš„å½±å“。一旦新期æƒçš„æ‰¹å‡†è¢«å…¬å¸ƒï¼Œè‚¡ç¥¨ä»·æ ¼ä¼šè¿…é€Ÿå¯¹è¿™æ¡æ¶ˆæ¯è¿›è¡Œå……分的调整,这时已ç»è€ƒè™‘到了稀释å‘生的å¯èƒ½æ€§ã€‚è¿™æ„味ç€åªè¦æ˜¯åœ¨å…¬å¸ƒä¹‹åŽè¿›è¡Œä¼°å€¼ï¼Œé‚£ä¹ˆç¨€é‡Šçš„å½±å“å°†ä¸å¤å˜åœ¨ã€‚2004å¹´çš„FAS 123没有给出清楚的指导。由于FASBå‡ ä¹Žæ²¡æœ‰å¯¹ç¨€é‡Šç»™å‡ºæŒ‡å¯¼(A39)ã€è€ƒè™‘äº†ç¨€é‡Šæ—¶é¢„æµ‹è‚¡ç¥¨ä»·æ ¼æ˜¯éžå¸¸å›°éš¾çš„ã€ç¨€é‡Šçš„å½±å“是éžå¸¸å¾®å°çš„(å…¶åªå 股票总é‡ä¸çš„很å°æ¯”例),故而稀释的影å“å¯ä»¥è¢«å¿½ç•¥ä¸è®¡ã€‚

图1.23 零罚没率的情况下使用二å‰æ ‘结果æ¥ç¡®å®šé¢„期生命周期
将蒙特å¡ç½—模拟è¿ç”¨äºŽç»Ÿè®¡ç½®ä¿¡åº¦å’Œç²¾åº¦æŽ§åˆ¶
下一æ¥ï¼Œè’™ç‰¹å¡ç½—模拟å¯ä»¥è¢«è¿ç”¨äºŽèŽ·å–股票期æƒå…¬å…价值的估计范围。å³å¦‚果股票期æƒçš„输入值是ä¸ç¡®å®šçš„并且是éšæœºçš„,那么就å¯ä»¥å¯¹å…¶è¿ç”¨è’™ç‰¹å¡ç½—模拟。我们å¯ä»¥å°†åˆ†å¸ƒå‡è®¾è¿ç”¨äºŽè¿™äº›å˜é‡ï¼Œå¹¶ä¸”用BSMã€GBM得到的期æƒä»·å€¼çš„结果ã€å¯¹è·¯å¾„的模拟ã€äºŒå‰æ ‘模型å¯ä»¥è¢«é€‰ä½œé¢„测å•å…ƒæ ¼ã€‚
模拟的结果在本质上是股票期æƒä»·å€¼çš„分布。我们必须注æ„,æ¤å¤„的模拟仅仅是用æ¥åŒºåˆ«ä¸åŒçš„输入值,从而获å–输出结果的范围,而ä¸æ˜¯ä¸ºäº†è®¡ç®—期æƒçš„价值。然而,模拟既å¯ä»¥è¢«ç”¨æ¥æ¨¡æ‹Ÿè¾“入值从而获å–期æƒç»“果的范围,也å¯ä»¥é€šè¿‡ç‹¬ç«‹è·¯å¾„模拟解决期æƒçš„模型问题。例如:模拟的输入值是那些具有高度ä¸ç¡®å®šæ€§å¹¶ä¸”在未æ¥ä¼šå‘生改å˜çš„值(å¦‚æ‰¹å‡†æ—¥çš„è‚¡ç¥¨ä»·æ ¼ã€æ³¢åŠ¨æ€§ã€å¤±æ•ˆçŽ‡ã€æ¬¡ä¼˜æ‰§è¡Œä¹˜æ•°ç‰)。显然,客观的å˜é‡å¦‚æ— é£Žé™©åˆ©çŽ‡(美国会公布期é™ä»Ž1个月到20年的国债的收益率)ã€çº¢åˆ©æ”¶ç›Š(è¿™å–决于公å¸çš„战略)ã€ç‰å¾…期ã€åˆçº¦ä»·æ ¼ã€ä¸æ–期é™(è¿™å–决于期æƒåˆçº¦ä¸çš„规定)ç‰æ˜¯ä¸åº”该被模拟的。æ¤å¤–,模拟的输入å‡è®¾æœ‰å¯èƒ½æ˜¯ç›¸å…³çš„ã€‚ä¾‹å¦‚ï¼šå¤±æ•ˆçŽ‡ä¸Žè‚¡ç¥¨ä»·æ ¼å‘ˆè´Ÿç›¸å…³â€”â€”å¦‚æžœå…¬å¸è¿ä½œå¾—ä¸é”™ï¼Œåˆ™è‚¡ç¥¨ä»·æ ¼ä¼šæ高,这使得期æƒæ›´æœ‰ä»·å€¼ï¼Œè¿™æ ·å°±ä¼šä½¿å‘˜å·¥ä¸å€¾å‘于离开公å¸ä¸”å…¬å¸ä¹Ÿä¸å€¾å‘于解雇员工。最åŽï¼Œè¾“出值的预测是期æƒä¼°å€¼çš„结果。事实上,FAS 123(B64ã€B65以åŠè„šæ³¨48ã€52ã€74ã€97)å…许并推è蒙特å¡ç½—模拟。
图1.24是对所有å˜é‡è¿ç”¨è‡ªå®šä¹‰äºŒå‰æ ‘模型(基于å•ç‚¹è¾“入值)计算出的结果。模型采用了外æ¥è¾“入值(如:待æƒæœŸã€å¤±æ•ˆçŽ‡ã€æ¬¡ä¼˜æ‰§è¡Œä¹˜æ•°ã€ä¸æ–期é™),并且éšç€æ—¶é—´è€Œæ”¹å˜è¾“入值(红利ã€æ— 风险利率ã€æ³¢åŠ¨æ€§)。期æƒä»·å€¼çš„结果是$31.42。这个分æžå¯ä»¥è¢«æ‰©å±•ï¼Œä»Žè€Œä½¿å…¶åŒ…括模拟。图1.25显示的是伴éšæœ‰è‡ªå®šä¹‰äºŒå‰æ ‘模型的模拟结果(Risk Simulator®软件被用于模拟输入å˜é‡)。
è½¯ä»¶ä¼šè‡ªåŠ¨æ ¹æ®ç»Ÿè®¡æ˜¾è‘—性和精度控制的è¦æ±‚确定试验é‡å¤çš„次数,而ä¸æ˜¯éšæœºåœ°å†³å®šåœ¨æ¨¡æ‹Ÿä¸è¯•éªŒè¿›è¡Œçš„次数。本例ä¸ç½®ä¿¡åº¦ä¸º99.9%,精度控制为.01,一共进行了145510次试验。这组éžå¸¸ä¸¥æ ¼çš„å‚数设置æ„味ç€éœ€è¦è¿›è¡Œè¶³å¤Ÿå¤šæ¬¡çš„试验æ‰èƒ½ä½¿ç»“果满足置信度为99.9%ã€ç²¾åº¦æŽ§åˆ¶ä¸º0.01。例如:模拟的平å‡ç»“果是$31.32(图1.25)。这æ„味ç€åœ¨1000次试验ä¸ï¼Œ999次的结果离$31.32的误差åªæœ‰.01。这些措施是在统计上有效的也是公æ£çš„。
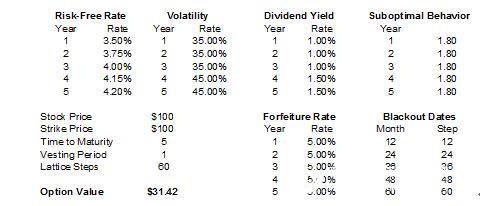
图1.24 使用定制二å‰æ ‘模型的å•ç‚¹è®¡ç®—结果
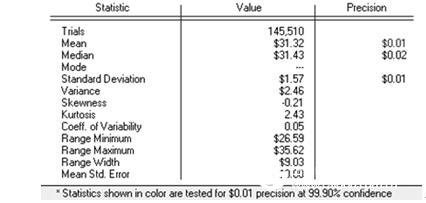
图1.25 99.9%置信区间和精度为0.01美元时期æƒçš„估值结果
æ¥æ•°
二(多)å‰æ ‘模型的æ¥æ•°è¶Šå¤šï¼Œç»“果的精度越高。图1.26显示的是è¿ç”¨BSMçš„é—åˆå½¢å¼çš„模型对没有红利的欧å¼çœ‹æ¶¨æœŸæƒè®¡ç®—出的收敛的结果(与基本的二å‰æ ‘模型的结果相比)。一般在1000æ¥åŽå¯ä»¥å¾—到收敛的结果。åŒæ ·åœ°ï¼Œå¦‚果有å¯èƒ½çš„è¯ï¼Œå°±åº”该使用1000æ¥çš„计算结果。由于需è¦å¾ˆå¤šçš„æ¥æ•°æ‰èƒ½å¾—到ç†æƒ³çš„结果,所以我们è¦è¿ç”¨åŸºäºŽè½¯ä»¶çš„æ•°å¦ç®—法。例如:1000æ¥çš„éžé‡ç»„二å‰æ ‘模型需è¦è®¡ç®—2×10301个节点,如果没有专门的算法,人工计算是ä¸å¯èƒ½çš„。图1.27显示的是用æ¸è¿‘å¢žåŠ çš„æ¥æ•°å¾—到的收敛结果(æ¯120æ¥ä¸ºä¸€ç»„)。计算出的数æ®è¢«åˆ¶æˆè¡¨æ ¼ï¼Œå¹¶ä¸”本例也给出了结果的ä¸ä½æ•°ã€‚在这个自定义二å‰æ ‘模型ä¸ï¼Œæœ€å¥½çš„估计是4200æ¥ï¼Œè¾“入的数值通用于整个分æžã€‚
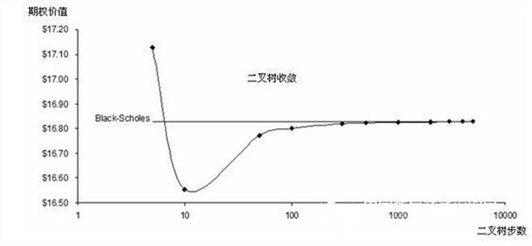
图1.26 二å‰æ ‘模型的计算结果趋åŒäºŽé—å¼æ–¹ç¨‹çš„计算结果
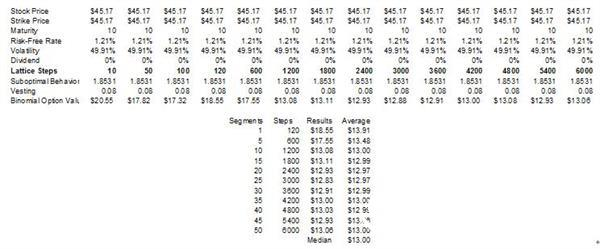
图1.27 定制二å‰æ ‘模型得到的收敛结果
in conclusion
自Fisher Blackã€Myron Scholesã€Robert Merton给出了他们的期æƒå®šä»·æ¨¡åž‹ä»¥åŠä¸ºé‡‘èžç•Œå¸¦æ¥å·¨å¤§çš„è¿›æ¥å·²ç»30多年了;å› æ¤ï¼Œä¸åº”该将股票期æƒå®šä»·å±€é™äºŽæŸä¸ªå…·ä½“çš„æ¨¡åž‹ï¼Œå› ä¸ºæˆ‘ä»¬æ€»èƒ½æŽ¢ç´¢åˆ°å…¶ä»–æ›´å¥½çš„æ¨¡åž‹ã€‚å¯¹è‚¡ç¥¨æœŸæƒè¿›è¡Œä¼°å€¼çš„三ç§ä¸»è¦æ–¹æ³•æ˜¯ï¼šé—åˆå½¢å¼çš„模型(如:BSMã€GBMã€ç¾Žå¼æœŸæƒè¿‘似模型)ã€è’™ç‰¹å¡ç½—模拟ã€äºŒå‰æ ‘模型。当å˜åœ¨æ¬¡ä¼˜è¡Œä¸ºã€ç‰å¾…期ã€å¤±æ•ˆçŽ‡æ—¶ï¼ŒBSM与GBM常常会高估ESOsçš„å…¬å…价值。事实上,如果用BSMå’ŒGBM对ESOs进行估值,那么这常常会高估真实æˆæœ¬ã€‚在è¿ç”¨BSM之å‰ï¼Œéœ€è¦æ»¡è¶³è®¸å¤šæ½œåœ¨å‡è®¾ï¼ŒåŒæ ·åœ°ï¼Œå®ƒä¹Ÿæœ‰è®¸å¤šæ˜Žæ˜¾çš„é™åˆ¶(这包括,它åªèƒ½è¢«è¿ç”¨äºŽæ— 红利的欧å¼æœŸæƒ)。æ¤å¤–,美å¼æœŸæƒè¿‘似模型éžå¸¸å¤æ‚ã€å¹¶ä¸”很难è¿ç”¨äºŽExcel的工作表。BSMä¸è€ƒè™‘美å¼æœŸæƒã€åŸºäºŽæ”¯ä»˜çº¢åˆ©çš„期æƒ(然而GBMå¯ä»¥åœ¨æ¬§å¼æœŸæƒä¸è€ƒè™‘红利)ã€å¤±æ•ˆçŽ‡ã€ä¸è‰¯ä¸šç»©ã€è‚¡ç¥¨ä»·æ ¼çš„é™åˆ¶ã€å¾…æƒæœŸã€ä¸æ–å˜åŒ–的商业环境和波动性ã€æ¬¡ä¼˜è¡Œä¸ºä»¥åŠä¸€äº›å…¶ä»–情况。蒙特å¡ç½—模拟å¯ä»¥å•ç‹¬ä½œä¸ºä¸€ç§å¯¹è‚¡ç¥¨æœŸæƒä»·æ ¼è¿›è¡Œä¼°å€¼çš„方法,但这仅é™äºŽæ¬§å¼æœŸæƒã€‚模拟有以下两ç§æ–¹å¼ï¼šé€šè¿‡å¯¹è‚¡ç¥¨ä»·æ ¼è·¯å¾„的模拟,从而计算出期æƒçš„å…¬å…价值;与其他方法(如:二å‰æ ‘模型和é—åˆå½¢å¼çš„模型)ååŒä½¿ç”¨ï¼Œä»Žè€Œæ‰¾å‡ºæ¨¡åž‹ä¸ä¸ç¡®å®šæ€§çš„æ¥æºã€‚
二å‰æ ‘模型具有稳定性并且易于è¿ç”¨ã€‚它å¯ä»¥è¢«è¿ç”¨äºŽå¯¹å¸¦æœ‰çº¢åˆ©çš„欧å¼æœŸæƒè¿›è¡Œä¼°å€¼ï¼Œä½†è¿™éœ€è¦è®¡ç®—能力。我们需è¦è¿ç”¨è½¯ä»¶æ¥æ‰§è¡Œè¿™ç§è¿ç®—。二å‰æ ‘模型å¯ä»¥è¢«ç”¨äºŽè®¡ç®—支付红利的美å¼æœŸæƒï¼Œå¯ä»¥å¾ˆå®¹æ˜“åœ°è¢«æ”¹é€ ä»¥è§£å†³å¸¦æœ‰å¤–æ¥è¾“入值的ESOs问题,å¯ä»¥ä¸Žè’™ç‰¹å¡ç½—模拟ååŒè¿ç”¨ä»¥è€ƒè™‘ä¸ç¡®å®šçš„输入å‡è®¾(失效的概率ã€æ¬¡ä¼˜è¡Œä¸ºã€è½¬æ‰‹ã€ä¸è‰¯ä¸šç»©),å¯ä»¥ç”¨äºŽè®¡ç®—é«˜ç²¾åº¦çš„ç½®ä¿¡åŒºé—´ã€‚åŸºäºŽæœ¬æ¡ˆä¾‹ç ”ç©¶æ‰€åšçš„分æžï¼Œæˆ‘们建议在使用模型时,请先确认ESO是欧å¼çš„。事实上,带有外æ¥è¾“å…¥å˜é‡çš„美å¼æœŸæƒæ˜¯ä¸å…è®¸è¢«ä½¿ç”¨çš„ï¼Œå› ä¸ºè¿™ä¼šå¤§å¤§åœ°é«˜ä¼°è¡¥å¿æˆæœ¬ã€‚å½±å“ESOsçš„å…¬å…ä»·å€¼çš„å› ç´ æœ‰å¾ˆå¤šï¼Œæˆ‘ä»¬åº”è¯¥è¿ç”¨è€ƒè™‘è¿™äº›å› ç´ çš„äºŒå‰æ ‘模型。åªè¦ç»è¿‡è®¤çœŸçš„å¦ä¹ ,就å¯ä»¥åƒåœ¨æœ¬æ¡ˆä¾‹ç ”究ä¸æ‰€æ¼”ç¤ºçš„é‚£æ ·è¿ç”¨äºŒå‰æ ‘模型对ESOs进行估值,本例所使用的方法是注é‡å®žæ•ˆçš„ã€ç²¾ç¡®çš„并且是在ç†è®ºä¸Šåˆç†çš„。
Live Animal Cage Trap,Medium Cage Trap,Large Cage Trap,Animal Cage Trap
Hebei Liebang Metal Products Co.,Ltd , https://www.lb-animaltraps.com
